The "ladder paradox" is not a paradox in and of itself, but rather a thought experiment that is often used to illustrate the concept of length contraction in special relativity.
The basic idea of the ladder paradox is as follows: imagine that there is a ladder lying flat on the ground, and two observers, A and B, are standing on opposite sides of the ladder. Observer A is stationary, while observer B is moving past the ladder at a high speed. According to the theory of special relativity, lengths appear to be contracted in the direction of motion, so observer B should see the ladder as being shorter than it appears to observer A. However, if observer B were to measure the length of the ladder using a measuring tape, they would find that the ladder is actually longer than it appears.
The paradox arises because it seems as though there are two contradictory statements: on the one hand, the ladder appears to be shorter to observer B due to length contraction, but on the other hand, it is actually longer when measured with a tape measure. However, this apparent contradiction can be resolved by taking into account the relative motion of the observers and the effects of time dilation. In short, the length of the ladder is not an absolute quantity, but depends on the frame of reference of the observer making the measurement.
To explain the ladder paradox in more detail, let's consider a specific example. Suppose that the ladder is 10 meters long when measured by observer A, who is standing still relative to the ladder. Observer B is moving past the ladder at a velocity of 0.6 times the speed of light (i.e., 180,000 km/s). According to special relativity, the length of the ladder as seen by observer B will be contracted by a factor of γ = 1/√(1-v^2/c^2), where v is the velocity of observer B relative to the ladder and c is the speed of light. In this case, γ = 0.8, so observer B will see the ladder as being only 8 meters long.
However, if observer B were to measure the length of the ladder using a tape measure, they would find that it is actually longer than 8 meters. This is because the tape measure itself is subject to length contraction when viewed from observer A's frame of reference. Specifically, the tape measure will appear to be shorter when moving past observer A at a high speed, just as the ladder appears to be shorter when viewed from observer B's frame of reference.
To calculate the actual length of the ladder as measured by observer B, we need to take into account the effects of time dilation. According to special relativity, time appears to run slower in a moving frame of reference than in a stationary one. As a result, observer B will measure the length of the ladder over a longer period of time than observer A, and this extra time will compensate for the length contraction. Specifically, the time dilation factor for observer B is given by δ = 1/√(1-v^2/c^2), which in this case is δ = 1.25. This means that observer B will measure the length of the ladder over a time interval that is 1.25 times longer than the time interval measured by observer A.
Using these factors, we can calculate the actual length of the ladder as measured by observer B. If observer B measures the length of the ladder over a time interval of 12.5 seconds (i.e., 10 seconds multiplied by the time dilation factor of 1.25).
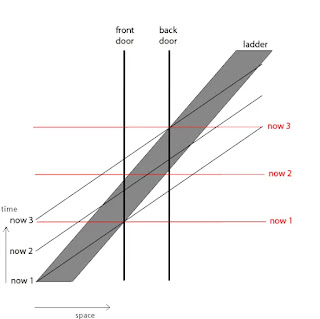
Further understanding of the ladder paradox can be gained by considering the concept of relativity of simultaneity. According to this principle, events that appear to happen simultaneously in one frame of reference may not appear simultaneous in another frame of reference that is moving relative to the first. In the case of the ladder paradox, this means that the positions of the ends of the ladder at a given moment in time may appear different to observers in different frames of reference.
To illustrate this, let's return to the example of the ladder being 10 meters long when measured by observer A. Suppose that observer A observes the front end of the ladder to be at position x=0 and the back end to be at position x=10 meters. However, from observer B's perspective, the ladder is moving at a high speed and the positions of the ends of the ladder will appear different due to relativity of simultaneity.
To calculate the positions of the ends of the ladder as seen by observer B, we need to take into account the fact that the front end of the ladder will reach observer B before the back end does. Specifically, we need to calculate the time interval between the front end of the ladder passing observer B and the back end of the ladder passing observer B. This time interval is given by Δt = Δx/v, where Δx is the distance between the front and back ends of the ladder as measured by observer B, and v is the velocity of observer B relative to the ladder.
Using the length contraction factor γ and the time dilation factor δ as before, we can calculate that the distance between the ends of the ladder as seen by observer B is Δx = γ(10 meters) = 8 meters. The velocity of observer B relative to the ladder is v = 0.6c, where c is the speed of light. Thus, the time interval between the front and back ends of the ladder passing observer B is Δt = Δx/v = (8 meters)/(0.6c) = 13.3 nanoseconds.
Now, let's suppose that observer B has two clocks, one at the front end of the ladder and one at the back end. According to the relativity of simultaneity, these clocks will not appear to be synchronized in observer A's frame of reference, because the positions of the ends of the ladder appear different to observer A. Specifically, the clock at the front end of the ladder will appear to be ahead of the clock at the back end of the ladder.
To calculate the time difference between the clocks as seen by observer A, we need to take into account the time it takes for light signals to travel from the clocks to observer A. Specifically, we need to subtract the time it takes for the light signal from the back end of the ladder to reach observer A from the time it takes for the light signal from the front end of the ladder to reach observer A. This time difference is given by Δt' = Δt - Δx/c, where Δt is the time interval calculated above and Δx/c is the time it takes for the light signal from the back end of the ladder to reach observer A.
Using the values calculated above, we can find that Δt' = 13.3 nanoseconds - (10 meters)/(3x10^8 m/s) = 13.3 nanoseconds - 33.3 picoseconds = 13.3 nanoseconds (to the nearest nanosecond). Thus, according to observer A, the clock at the front end of the ladder is ahead of the clock at the back end by 13.3 nanoseconds.
the ladder paradox also illustrates the relativity of simultaneity, which shows that events that appear to happen simultaneously in one frame of reference may not appear simultaneous in another frame of reference that is moving relative to the first. This principle is a fundamental consequence of the postulates of special relativity, which assert that the laws of physics are the same in all inertial frames of reference , and that the speed of light is constant in all frames of reference.
The ladder paradox also has important implications for the concept of time dilation in special relativity. Time dilation refers to the fact that time appears to pass more slowly for objects that are moving relative to an observer than for stationary objects. This effect is due to the fact that moving clocks appear to run more slowly than stationary clocks, as predicted by the time dilation factor δ.
To see how the ladder paradox relates to time dilation, let's consider a different scenario in which the ladder is stationary in observer A's frame of reference, but is moving relative to observer B at a velocity of 0.6c. Suppose that observer A has a clock that is synchronized with the front end of the ladder, and that observer B has a clock that is synchronized with the back end of the ladder.
According to the time dilation factor δ, the clock at the back end of the ladder will appear to run more slowly than the clock at the front end of the ladder, because the back end of the ladder is moving relative to observer A. Specifically, the time that appears to elapse on the clock at the back end of the ladder as seen by observer A is given by δΔt, where Δt is the time that appears to elapse on the clock at the front end of the ladder, and δ is the time dilation factor given by δ = 1/γ.
Using the length contraction factor γ as before, we can calculate that γ = 0.8, which means that δ = 1/0.8 = 1.25. Thus, the time that appears to elapse on the clock at the back end of the ladder as seen by observer A is 1.25 times longer than the time that appears to elapse on the clock at the front end of the ladder.
Now, let's suppose that the ladder is 10 meters long in observer A's frame of reference, and that the clock at the front end of the ladder ticks once every second. According to observer A, it takes 10 seconds for the front end of the ladder to reach the back end of the ladder. However, from observer B's perspective, the ladder is moving at a high speed, and the time interval between the front end of the ladder passing observer B and the back end of the ladder passing observer B is longer than 10 seconds due to time dilation.
To calculate the time interval between the front and back ends of the ladder passing observer B, we need to take into account the time dilation factor δ. Specifically, the time that appears to elapse on the clock at the back end of the ladder as seen by observer B is given by δΔt', where Δt' is the time that appears to elapse on the clock at the front end of the ladder as seen by observer B.
Using the values calculated above, we can find that Δt' = Δt/δ = 1 second. Thus, from observer B's perspective, the front end of the ladder takes 1 second to reach the back end of the ladder. However, because the distance between the ends of the ladder appears shorter to observer B due to length contraction, the speed of the ladder as seen by observer B is faster than the speed of light as seen by observer A.
This apparent violation of speed of light limit is not a true This apparent violation of the speed of light limit is not true violation because it is based on a faulty assumption that the two events of the front and back end of the ladder passing a stationary observer B are simultaneous. In reality, due to the relativity of simultaneity, the two events are not simultaneous in observer A's frame of reference, which means that the ladder does not actually exceed the speed of light as seen by observer A.
In summary, the ladder paradox is a thought experiment that highlights some of the counterintuitive effects of special relativity, such as length contraction, time dilation, and the relativity of simultaneity. While the paradox may seem confusing or even contradictory at first, it can be explained using the principles of special relativity and provides important insights into the nature of space, time, and motion.




0 Comments
Post a Comment